Write a key-value store from scratch
I was reading Designing Data Intensive Applications, and I thought it would be worthwhile to implement a key-value store from the ground-up using the principles described in the book.
The following outlines my understanding of the rationale, the algorithmic analyses, and the implementation design of the engine.
A working implementation with tests and docs can be found here
The motivation
The memory space of a traditional hashmap is more or less bounded by RAM. For storing large datasets, this is quite likely insufficient. The only way to then persist data would be by writing it to disk.
Thus, the question is: how do we optimally lay out the data in disk for fast insertions and retrievals?
There’s many pproaches to solve this problem. SQL is based on the concept of B-Trees, Riak is based on Bitcask. We’ll look at a design that’s used by databases like LevelDB – one based on Sorted-String Tables (SST).
The Idea
The high-level idea is to maintain an in-memory data structure such as a red-black tree (typically termed memtable) that can hold entries up to a certain threshold (eg: t<=RAM). At the breaking point, all entries are dumped into a file in sorted order (the rationale for this will become evident later)
The resulting file is immutable and termed a Sorted-String Table (SST). The memtable is then cleared, and the process repeats; we also keep track of segments created thus far.
Periodically, these segments are merged in order to save space and remove duplicates.
 Merging segments into a new segment with most recent values [1]
Merging segments into a new segment with most recent values [1]
So, for every get(key)
query, we first look into the memtable for the corresponding value; if the entry isn’t present, we read into our SST files (there can be more than one!), starting from the most recent one.
At first, this seems like it runs in O(entries) in the worst-case, as we’d have to linearly scan through the SST(s).
(In the best case, the entry is held in the memtable, and retrieving it would run in O(log(in_memory_size)). Here in_memory_size refers to the maximum number of entries that can be held in the memtable; for large datasets, entries >> inmemory_size)
However, if we know the max size of all entries ahead of time, we can simply perform a binary search on the SST, as the file is sorted (it’s in the name!) and we know exactly how much to jump between any two entries. This would run in O(log(entries))
The downside with this is that it trades away a lot of flexibility for the user: it isn’t always possible to predict that the size of your data ahead of time, nor is it always possible to enforce one.
So: how do we design the engine such that it provides flexibility while still performing better than a linear scan through the disk?
Optimizations
In addition to maintaining a memtable, we also maintain a data structure known as a sparse memory index (SMI).
The rationale is the following:
Given a query and a file containing a list of n sorted entries, if we know the offsets of every m entries in our SMI, we can jump to the entry that’s closest to the query, then scan forward until we find a the entry whose key is bigger than the query.
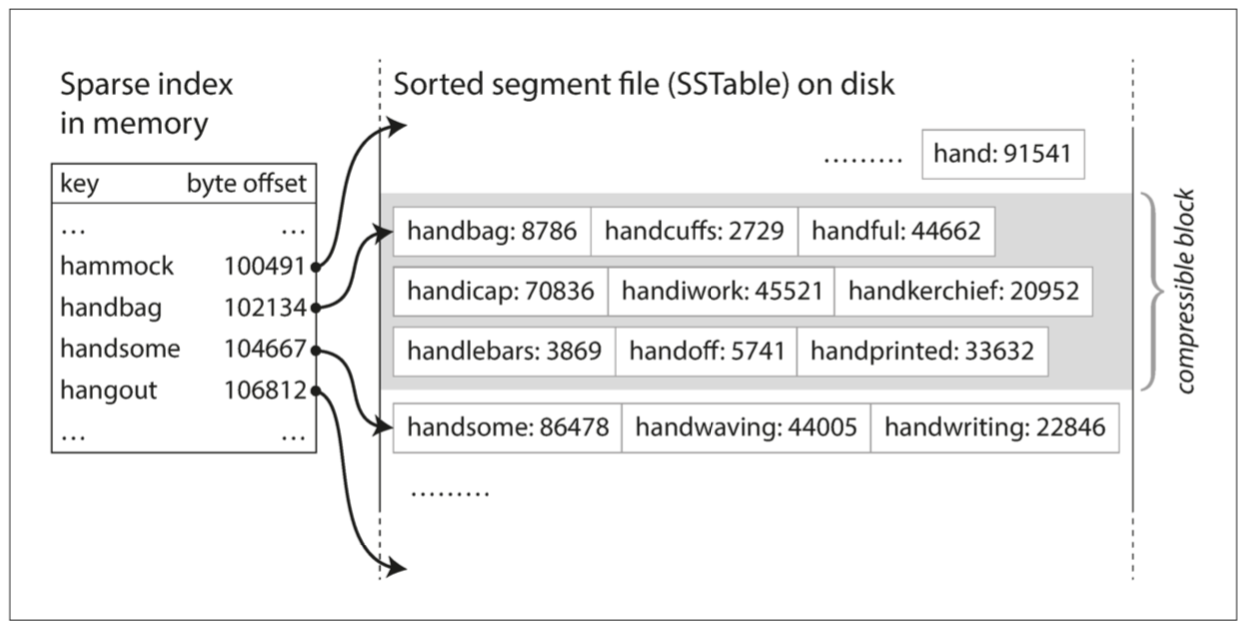 If we’re looking for “handicap”, and we know the offsets for “handbag” and “handsome”, we can restrict the range of entries to iterate over [2]
If we’re looking for “handicap”, and we know the offsets for “handbag” and “handsome”, we can restrict the range of entries to iterate over [2]
This is quite efficient. The space taken by the SMI is O(n/m). Looking up the closest key is bound by O(log(n/m)) (as long as it’s built on top of a red-black BST), and scanning through the file runs in O(m).
With a decent parameter setting for m (eg: storing one out of every 150 entries), such a design is quite likely to work well in practice.
The problem with the above approach is that we could still run into a case where we try to find a key that doesn’t exist in the DB. We’d be unnecessarily looking into all segments (at worst), trying to find an entry with a key that wasn’t inserted in the first place.
Fortunately, this can be easily mitigated using a (dynamically-scaled) bloom-filter. It’s space-efficient enough that we can get away with having it store all keys (it doesn’t actually store keys, it stores their hashes), and it will tell us with absolute certainty if a key is absent from the db. Perfect!
Additional Optimizations
There’s still a few other optimizations worth exploring:
-
dynamically determine when best to merge segments
-
Run the merging algorithm in a background thread
In the implementation, we hold a static field representing the maximum number of segments to be kept intact before merging. As soon as the number of segments reaches this threshold, all segments are merged. This is not always ideal: consider a scenario where we have 2 segments, both of which have a lot of overlapping keys, but the threshold is set to, say, 10. It makes sense to have those two segments merged first; waiting until 10 segments have been created would result in a lot of wasted space.
With regards to (2): it’s a bit unfortunate that the implementation is python; GIL constraints dictate that only thread can run at a time, so a background thread wouldn’t really help outperform the synchronous version. In other languages (like Rust or Go), this strategy would likely work out. (Actually,the merging algorithm involves quite a lot of file IO – maybe there’s scope for cooperative multi-tasking with coroutines?).
All in all, this turned out be a fun project that I quite enjoyed implementing.
References
[1] Designing Data Intensive Applications, page 74
[2] Designing Data Intensive Applications, page 76